Which Situation Could Be Modeled Using a Geometric Sequence

Use this space for 9 What is the inverse of the function y 4x 5. B Davids parents have set.

Contemporary Geometric Beadwork An Open Source Architectural Beadwork Project From Kate Mckinnon And A Worldwide Team Of In Bead Work Geometric Kate Mckinnon

Why can so many situations be modeled by exponential growth.

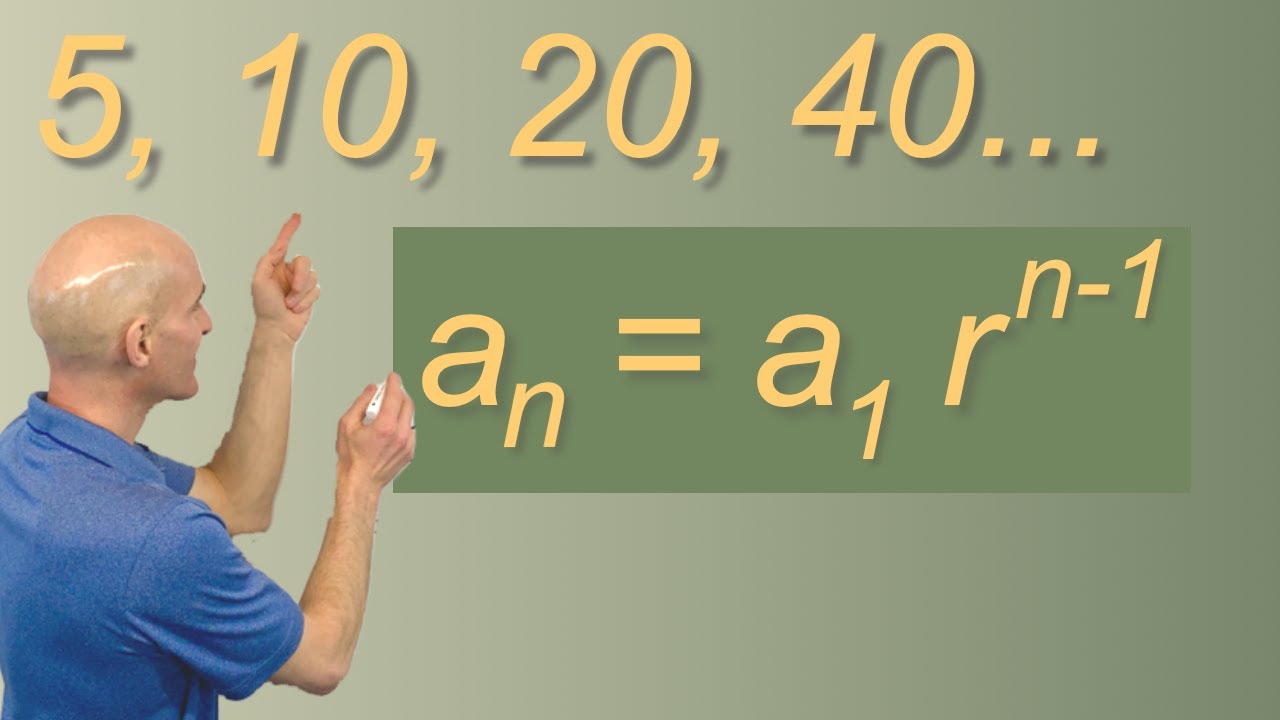
. The yearly salary values described form a geometric sequence because they change by a constant factor each year. A The temperature in your car is 797979. 27 Which situation could be modeled using a geometric sequence.

An exponential function is a function of the form a n where a 1 and n is a variable. Geometric Sequence Formula Youtube Geometric Model An Overview Sciencedirect Topics. A1 the first term of the sequence or the starting point.

The completely factored form of n 4 - 9n 2 4n 3 - 36n 12n 2 108 is. 2 Amount of cakes in bake sale increases by 3 each year the fundraiser is held. Write a recursive formula for the.

Up to 24 cash back To find the total sum of all of the terms this equation can be used-----. 1 m1 2000 mn mn 1 320 3 m1 2000 mn 084mn 1 2 mn 2000084 n 1 4 m n 2000084 n 1 10 Which situation could be modeled. Here is a great lessonactivity for using geometric sequences to model real world problems.

Feel free to usemodify this lesson plan to meet the needs of your students. The situation can be modeled by a geometric sequence with an initial term of 284. Here is the trick or recipe.

Group 5 Examples of Arithmetic Sequence in a Real Life Situation Problem 1 Kircher is practicing her dance steps for the competitionShe starts practicing the steps for 1. Mathematicians calculate a term in the series by. How can this sequence best be modeled recursively.

This is a geometric sequence with a common ratio of 2 and an exponential. Unit High School Mathematics Unit Title. Lets take a look at the sequence 18 36 72 144 288 18 36 72 144 288.

Which situation could be modeled using a geometric sequence. Which situation could be modeled using a geometric sequence. Which Situation Could Be Modeled Using a Geometric Sequence.

1 x __1 4 y __5 4 3 y 4x 5 2 y __1 4 x __5 4 4 y _____1 4x 5 10 Which situation could be modeled using a. Using the examples other people have given. Why is important to consider the limitations of an.

Each term of a geometric sequence increases or decreases by a. Geometric Sequences can be thought of as exponential equations with their domains restricted to integers. 1 x __1 4 y 5 4 3 y 4x 5 2 y __1 4 x 5 4 4 y _____1 x 5 10 Which situation could be modeled using a geometric.

1 Amount of cell phone users increases by 33 every year. Amount of cakes is. So they can model situations that involve a constant rate of.

Know how to use. The yearly salary values described form a geometric sequence because they change by a constant factor each year. Use this space for 9 What is the inverse of the function y 4x 5.

Each term of a geometric sequence increases or decreases by a. Note that if a sequence starts with a 5 then increases by 3 from one term to the next this situation can be modeled using a linear equation with 5 as its y-intercept and 3 as its. 1 A cell phone company charges 3000 per month for 2 gigabytes of data and 1250 for each additional gigabyte of.

Recognize and solve problems that can be modeled using finite geometric sequences and series such as home mortgage and other compound interest examples. Power to the Variable Page 3 of. An a1rn1 a n a 1 r n 1.

The student population will be 104 of the prior year so the common ratio is 104. Geometric progressions happen whenever each. 10 Which situation could be modeled using a geometric sequence.

Its a geometric sequence because the number of users are increasing exponentially every year. 1 A cell phone company charges 3000 per month for 2 gigabytes of data and 1250 for each additional gigabyte of. Many geometric sequences can me modeled with an exponential function.

There are many uses of geometric sequences in everyday life but one of the most common is in calculating interest earned. I like to explain why arithmetic and geometric progressions are so ubiquitous. You lower the temperature of your air conditioning by 222every 333 minutes in order to find a comfortable temperature.

S the total sum of all the terms.

Geometric Model An Overview Sciencedirect Topics

Geometric Model An Overview Sciencedirect Topics

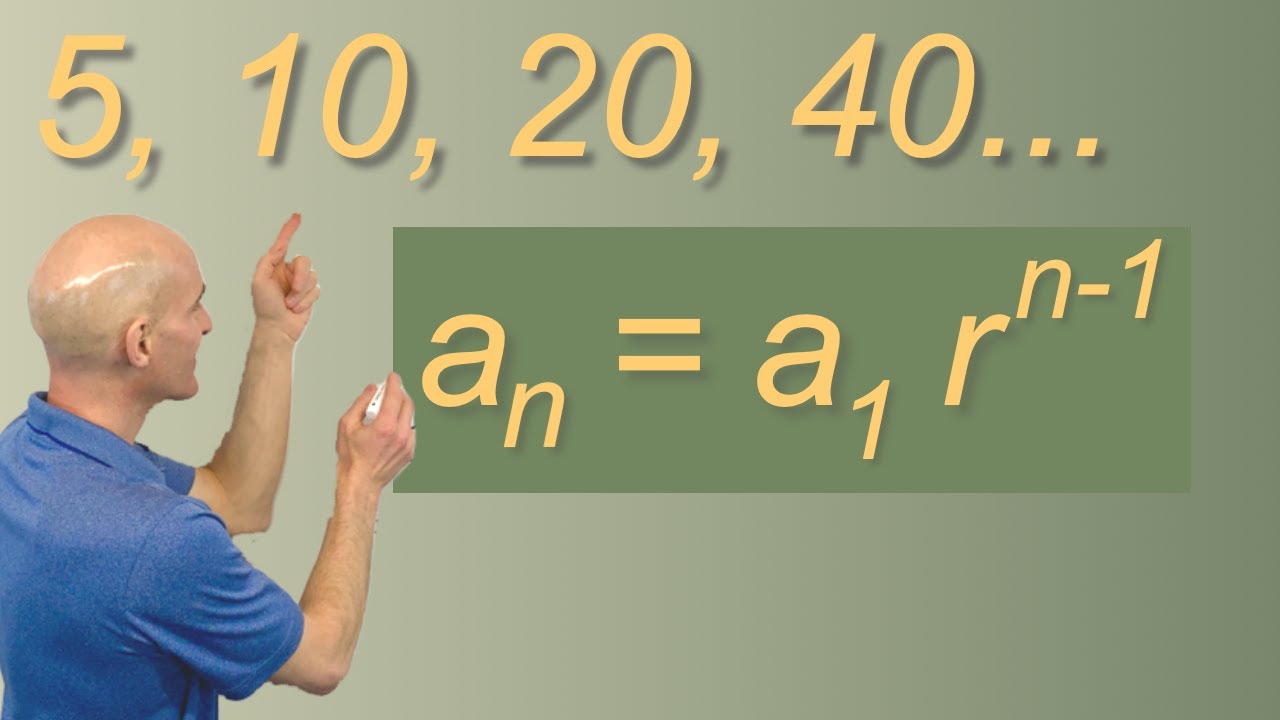
Geometric Sequence Formula Youtube

The Importance Of Eigenvalues And Eigenvectors Application What Does This Physically Mean Http Math Stackexchange C Short Answers Understanding Knowledge